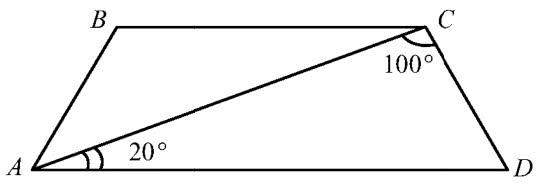
Найдите угол ABC равнобедренной трапеции ABCD, если диагональ AC образует с основанием AD и боковой стороной CD, углы равные 20 и 100 соответственно градусов.
Решение:
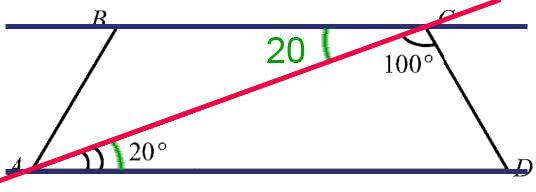
В трапеции две стороны параллельны:
AD параллельна BC
AC секущая
Углы BCA и CAD равны, как накрест лежащие. Они равны 20 градусам.
Так как по условию задачи трапеция равнобедренная:
Углы ABC и BCD равны.
Угол BCD=20+100=120, следовательно и угол ABC=120 градусов.
Ответ: угол ABC=120 градусов
Подписывайтесь на канал на YOUTUBE и смотри видео, готовься к экзаменам по математике и геометрии с нами.
Рекомендуем подписаться на новостную рассылку нашего сайта TutoMath.ru, чтобы быть в курсе всех новинок.
Хочешь готовиться к экзаменам бесплатно? Репетитор онлайн бесплатно. Без шуток. ЗДЕСЬ