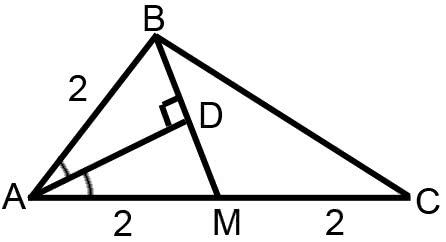
Прямая AD, перпендикулярна медиане BM треугольника ABC, делит угол BAC пополам. Найдите сторону AB, если сторона AC 4.
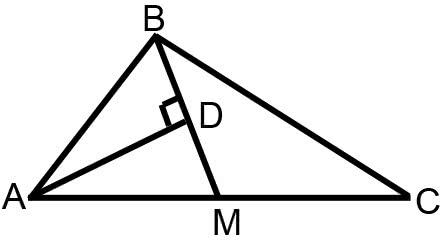
Решение:
AD — биссектриса, так как по условию сказано, что делит угол BAC пополам. От сюда следует, что углы DAM и DAB равны.
Так как по условию AD также является высотой. AD — общая сторона. Следовательно, треугольники ADM и ADB прямоугольные и из выше сказанного по равенству прямоугольных треугольников они равны.
Следовательно, AB=AM.
AM составляет половину стороны AC, так как BM — медиана.
Медиана треугольника ― отрезок соединяющий вершину треугольника с серединой противоположной стороны.
Биссектриса угла треугольника — отрезок, делящий угол на два равных угла длинной до пересечения с противолежащей стороной треугольника.
Высота треугольника -отрезок, опущенный из вершины треугольника перпендикулярно противоположной стороне.
AM=AC:2=4:2=2
AB=AM=2
Ответ: 2
Подписывайтесь на канал на YOUTUBE и смотри видео, готовься к экзаменам по математике и геометрии с нами.
Хотите готовиться к экзаменам бесплатно? Репетитор онлайн бесплатно. Без шуток. Кликните сюда, чтобы записаться на вебинар