Рациональные числа вы с ними уже знакомы, осталось только обобщить и сформулировать правила. Так какие числа называются рациональными числами? Рассмотрим подробно в этой теме урока.
Понятие рациональных чисел.
Определение:
Рациональные числа – это числа, которые можно представить в виде дроби \(\frac{m}{n}\), где m – целое число, а n – натуральное число.
Другими словами, можно сказать:
Рациональные числа – это все натуральные числа, целые числа, обыкновенные дроби, бесконечные периодические дроби и конечные десятичные дроби.
Разберем каждый пункт подробно.
- Любое натуральное число можно представить в виде дроби, например, число 5=\(\frac{5}{1}\).
- Любое целое число можно представить в виде дроби, например, числа 4, 0 и -2. Получаем 4=\(\frac{4}{1}\), 0=\(\frac{0}{1}\) и -2=\(\frac{-2}{1}\).
- Обыкновенные дроби уже записаны в рациональном виде, например, \(\frac{6}{11}\) и \(\frac{9}{2}\).
- Бесконечные периодические дроби, например, 0,8(3)=\(\frac{5}{6}\).
- Конечные десятичные дроби, например, 0,5=\(\frac{5}{10}=\frac{1}{2}\).
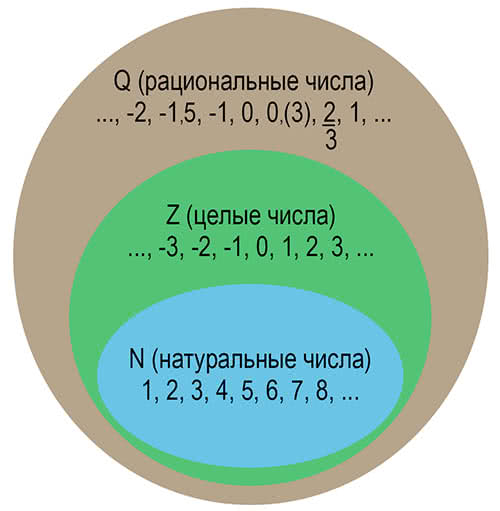
Множество рациональных чисел.
Вспомним, что множество натуральны чисел обозначается латинской буквой N.
Множество целых чисел обозначается латинской буквой Z.
А множество рациональных чисел обозначается латинской буквой Q.
Во множество рациональных чисел входит множество целых и натуральных чисел в этом и заключается смысл рациональных чисел.
На рисунке можно показать множество рациональных чисел.
Но не все числа являются рациональными. Бывают еще множества различных чисел, которые в дальнейшем вы будите изучать.
Бесконечные непрериодические дроби не принадлежат множеству рациональных чисел.
Например, число е, \(\sqrt{3}\) или число \(\pi\) (читается число пи) не являются рациональными числами.
Вопросы по теме «Рациональные числа»:
Какое выражение является рациональным числом из чисел \(\sqrt{5}, -0.(3), 15, \frac{34}{1569}, \sqrt{6}\) ?
Ответ:
Корень из 5 это выражение нельзя представить в виде конечно дроби или бесконечной периодической дроби, поэтому это число не рациональное.
Бесконечная десятичная периодическая дробь -0,(3)=\(-\frac{3}{10}\) можно представить в виде дроби, поэтому это рациональное число.
Число 15 можно представить в виде дроби \(\frac{15}{1}\), поэтому это рациональное число.
Дробь \(\frac{34}{1569}\) это рациональное число.
Корень из 6 это выражение нельзя представить в виде конечно дроби или бесконечной периодической дроби, поэтому это число не рациональное.
Записать число 1 в виде рационального числа?
Ответ: чтобы записать в виде рационального число 1 нужно представить его в виде дроби 1=\(\frac{1}{1}\).
Докажите, что число \(\sqrt{0,0049}\) является рациональным?
Доказательство: \(\sqrt{0,0049}=0,07\)
Является ли простое число под корнем рациональным числом?
Ответ: нет. Например, любое простое число под корнем 2, 3, 5, 7, 11, 13, … не выносится из под корня и его нельзя представить в виде конечно дроби или бесконечной периодической дроби, поэтому не является рациональным числом.