Основное свойство рациональных чисел достаточное простое для понятия. Пользоваться основным свойством дроби вы будите постоянно во всех классах и темах математики, поэтому важно его сейчас разобрать и понять.
Основное свойство дроби, приведение к общему знаменателю.
Определение:
Если числитель и знаменатель умножить на одно и тоже число, которое не равно нулю, то получится равная ей дробь.
Запишем формулу основного свойства рациональных чисел:
\(\bf \begin{align}\frac{p}{q}=\frac{p \times n}{q \times n}\end{align}\)Где p,q и n –целые числа (\(q \neq 0, n \neq 0\)).
По этой формуле приводят к общему знаменателю дроби. Умножаем на одно и тоже число числитель и знаменатель дроби.
Рассмотрим дробь, пример:
\(\begin{align}&\frac{1}{2}=\frac{1 \times 4}{2 \times 4}=\frac{4}{8} \\\\
&\frac{1}{2}=\frac{4}{8} \\\\
\end{align}\)
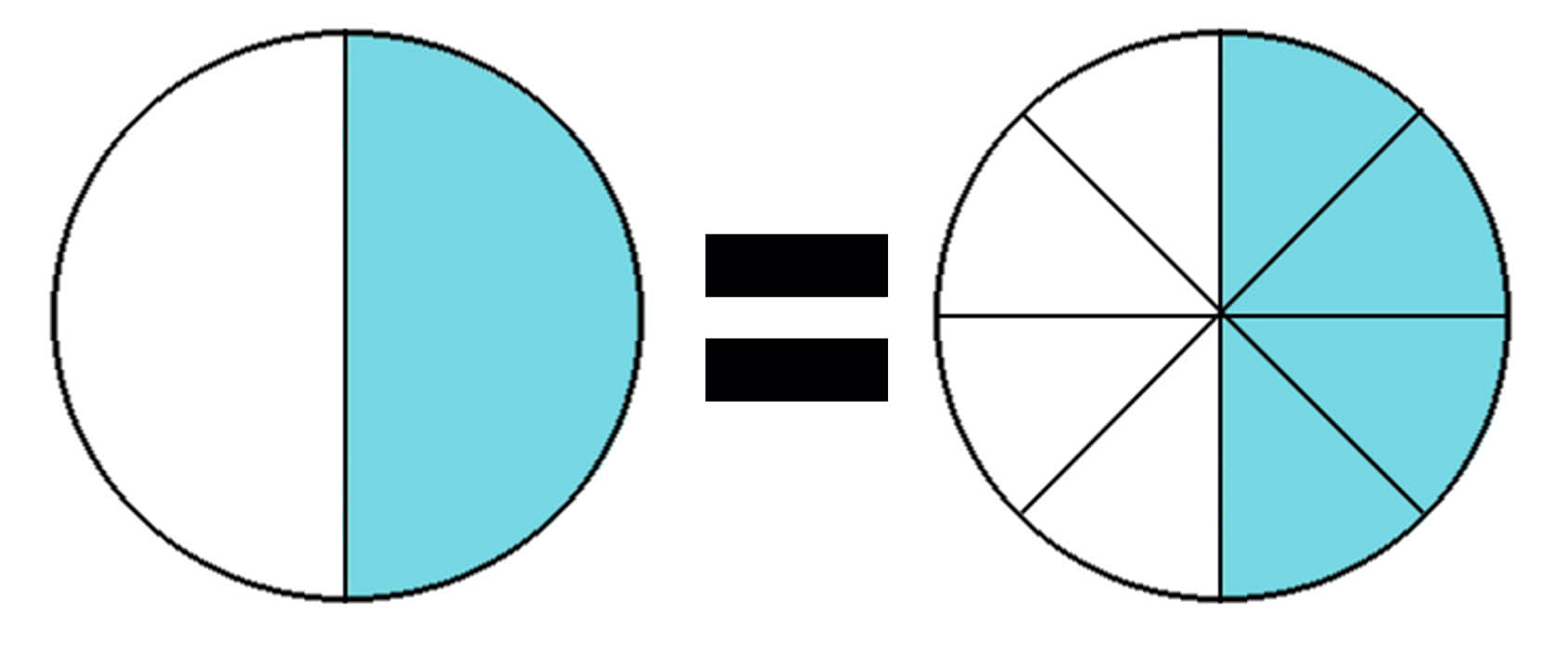
Разберем данные дроби на рисунке.
Видим, если мы круг раздели на две равные части и закрасим 1 часть из 2, то закрашенная часть круга будет равна 4 равным частям из 8.
В чем заключается смысл основного свойства, мы разобрали на примере. А теперь запишем краткие правила основного свойства дроби общего знаменателя:
- Числитель и знаменатель дроби умножаем на число отличное от нуля.
- Проверяем равны ли исходная дробь с полученной.
Основное свойство дроби, сокращение дробей.
Определение:
Если у дроби числитель и знаменатель делим на общий множитель, не равный нулю, то получиться равная ей дробь.
Запишем формулу основного свойства дроби.
\(\bf \begin{align}\frac{p \times n}{q \times n}=\frac{p}{q}\end{align}\)Где p,q и n –целые числа (\(q \neq 0, n \neq 0\)).
Такой вид формулы основного свойства дроби называется сокращением дробей. Мы имеем право сократить числитель и знаменатель на общий множитель.
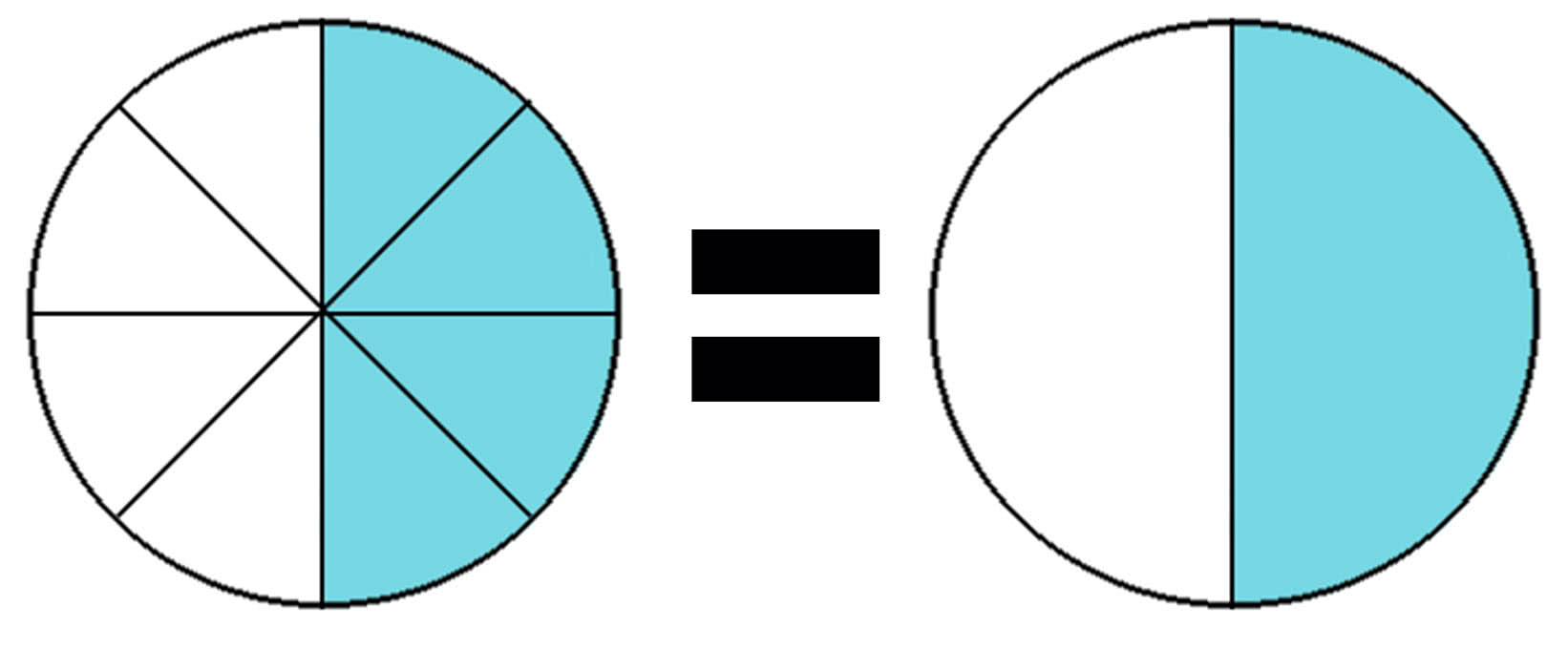
Рассмотрим ту же самую дробь, но в обратном порядке.
\(\begin{align}&\frac{4}{8}=\frac{1 \times 4}{2 \times 4}=\frac{1}{2} \\\\
&\frac{4}{8}=\frac{1}{2} \\\\
\end{align}\)
На рисунке запись дробей будет выглядеть так:
Основное свойство рациональных чисел сокращения дроби состоит из простых правил:
- Расписать числитель и знаменатель дроби на простые множители, найти среди них общий для числителя и знаменателя.
- Сократить числитель и знаменатель дроби на общий множитель.
- Проверяем равны ли исходная дробь с полученной.
Пример:
Пользуясь основным свойством дроби, найдите значение a, при котором верно равенство: а) \(\frac{a}{6}=\frac{8}{48}\) б) \(\frac{56}{70}=\frac{8}{a}\)
Решение:
а) \(\frac{a}{6}=\frac{8}{48}\)
Если мы внимательно посмотрим, то заметим, что знаменатель с числа 6 поменялся на число 48. Возникает вопрос: На какие число надо умножить 6, чтобы получить число 48? Ответ на 8, то есть первую дробь \(\frac{a}{6}\) числитель и знаменатель умножили на 8 и получили вторую дробь \(\frac{8}{48}\). Выглядит это так:
\(\begin{align}\frac{a}{6}=\frac{a \times 8}{6 \times 8}=\frac{8}{48}\end{align}\)Тогда возникает вопрос: Какое число скрывается под переменной а, при умножении на которую получаем 8. Не трудно догадаться, переменная a=1. Подставим и проверим:
\(\begin{align}\frac{1}{6}=\frac{1 \times 8}{6 \times 8}=\frac{8}{48}\end{align}\)А теперь рассмотрим, как решить пропорцию математически, ведь не всегда в выражении будут легкие числа.
\(\begin{align}&\frac{a}{6}=\frac{8}{48} \\\\
&a=\frac{8 \times 6}{48} \\\\
&a=\frac{48}{48} \\\\
&a=1 \\\\
\end{align}\)
Ответ: 1
б) \(\frac{56}{70}=\frac{8}{a}\)
Смотрим внимательно, видим, что в числители было число 56, а потом стало число 8. На какое число надо поделить 56, чтобы получить 8? Ответ на 7.
\(\frac{56}{70}=\frac{8 \times 7}{10 \times 7}=\frac{8}{10}=\frac{8}{a}\)Видим, что a=10. Теперь решим выражение \(\frac{56}{70}=\frac{8}{a}\) как пропорцию.
\(\begin{align}&\frac{56}{70}=\frac{8}{a} \\\\
&a \times 56=8 \times 70 \\\\
&a=\frac{8 \times 70}{56} \\\\
&a=\frac{560}{56} \\\\
&a=10
\end{align}\)
Ответ: 10