Следующее действие, которое можно выполнять с дробями это деление. Выполнять деление дробей достаточно просто главное знать несколько правил деления. Разберем правила деления и рассмотрим решение примеров на данную тему.
Деление дроби на дробь.
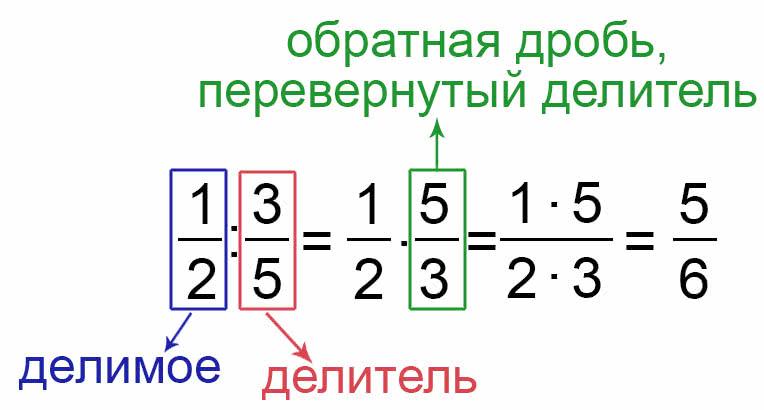
Чтобы делить дробь на дробь, нужно дробь, которая является делителем перевернуть, то есть получить обратную дробь делителю и потом выполнить умножение дробей.
\(\bf \frac{a}{b} \div \frac{c}{d} = \frac{a}{b} \times \frac{d}{c}\\\)Пример:
Выполните деление обыкновенных дробей .
Деление дроби на число.
Чтобы разделить дробь на число, нужно знаменатель дроби умножить на число.
\(\bf \frac{a}{b} \div n = \frac{a}{b} \div \frac{n}{1} = \frac{a}{b} \times \frac{1}{n}\\\)Рассмотрим пример:
Выполните деления дроби на натуральное число \(\frac{4}{7} \div 3\).
Как мы уже знаем, что любое число можно представить в виде дроби \(3 = \frac{3}{1} \).
\(\frac{4}{7} \div 3 = \frac{4}{7} \div \frac{3}{1} = \frac{4}{7} \times \frac{1}{3} = \frac{4 \times 1}{7 \times 3} = \frac{4}{21}\\\)Деление числа на дробь.
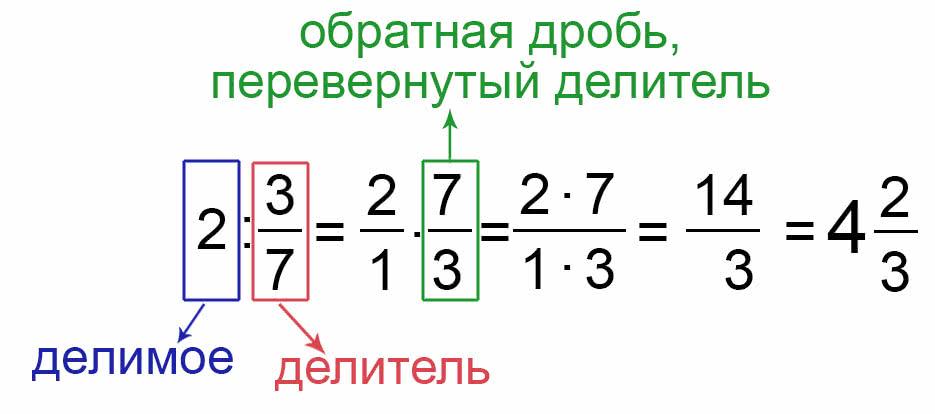
Чтобы поделить число на дробь, нужно знаменатель делителя умножить на число, а числитель делителя записать в знаменатель. То есть дробь делитель перевернуть.
Рассмотрим пример:
Выполните деление числа на дробь.
Деление смешанных дробей.
Перед тем как приступить к делению смешанных дробей, их нужно перевести в неправильную дробь, а дальше выполнить деление по правилу деления дроби на дробь.
Пример:
Выполните деление смешанных дробей.
\(2\frac{3}{4} \div 3\frac{1}{6} = \frac{11}{4} \div \color{red} {\frac{19}{6}} = \frac{11}{4} \times \color{red} {\frac{6}{19}} = \frac{11 \times 6}{4 \times 19} = \frac{11 \times \color{red} {2} \times 3}{2 \times \color{red} {2} \times 19} = \frac{33}{38}\\\)Деление числа на число.
Чтобы поделить простые числа, нужно представить их в виде дроби и выполнить деление по правилам деления дроби на дробь.
Пример:
\(2 \div 5 = \frac{2}{1} \div \color{red} {\frac{5}{1}} = \frac{2}{1} \times \color{red} {\frac{1}{5}} = \frac{2 \times 1}{1 \times 5} = \frac{2}{5}\\\)Примечание к теме деление дробей:
На нуль делить нельзя.
Вопросы по теме:
Как делить дроби? Как разделить дробь на дробь?
Ответ: дроби делятся так, первую дробь делимое умножаем на дробь обратную дроби делителя.
Как делить дроби с разными знаменателями?
Ответ: не важно одинаковые или разные знаменатели у дробей, все дроби делятся по правилу деления дроби на дробь.
Пример №1:
Выполните деление и назовите делитель, дробь, обратную делителю: а) \(\frac{5}{9} \div \frac{8}{13}\) б) \(2\frac{4}{5} \div 1\frac{7}{8}\)
Решение:
а) \(\frac{5}{9} \div \frac{8}{13} = \frac{5}{9} \times \frac{13}{8} = \frac{65}{72}\\\\\)
\( \frac{8}{13}\) – делитель, \( \frac{13}{8}\) – обратная дробь делителя.
б) \(2\frac{4}{5} \div 1\frac{7}{8} = \frac{14}{5} \div \frac{15}{8} = \frac{14}{5} \times \frac{8}{15} = \frac{14 \times 8}{5 \times 15} = \frac{112}{75} = 1\frac{37}{75}\\\\\)
\( \frac{15}{8}\) – делитель, \( \frac{8}{15}\) – обратная дробь делителя.
Пример №2:
Вычислите деление: а) \(5 \div 1\frac{1}{4}\) б) \(9\frac{2}{3} \div 8\)
Решение:
а) \(5 \div 1\frac{1}{4} = \frac{5}{1} \div \frac{5}{4} = \frac{5}{1} \times \frac{4}{5} = \frac{\color{red} {5} \times 4}{1 \times \color{red} {5}} = \frac{4}{1} = 4 \\\\\)
б) \(9\frac{2}{3} \div 8 = \frac{29}{3} \div \frac{8}{1} = \frac{29}{3} \times \frac{1}{8} = \frac{29 \times 1}{3 \times 8} = \frac{29}{24} = 1\frac{5}{24}\\\\\)