Решение линейных уравнений с одной переменной.
Рассмотри подробный алгоритм решения линейных уравнений с одной переменной.
Определение числовой функции. Область определения функции. Область значения функции.
Что такое область определения функции? что такое область значения функции? Давайте, в этой статье разберемся в понятиях числовой функции и ее характеристиках и свойствах. Определение...
Определение функции. Способы задания функции.
Что значить задать функцию? Какими способами можно задать функцию? Что такое определение функции? Задать функцию — это значит указать правило, при задании любого значения аргумента...
Десятичные дроби. Разряды и классы десятичных дробей.
Рассмотрим урок на тему десятичные дроби. Научимся записывать и читать десятичные дроби. А также разберем разряды и классы десятичных дробей. Вы уже знаете, что такое...
Что такое уравнение и корни уравнения? Как решить уравнение?
Уравнения бывают разные. Вы изучите их многие виды в курсе математике, но все они решаются по одним правилам, эти правила мы сейчас рассмотрим подробно. Что...
Деление рациональных чисел примеры и правила.
Деление рациональных чисел в математике имеет общий смысл, ведь понятие рациональные числа включает в себя все числа, которые в них входят (натуральные числа, целые числа,...
Квадратные неравенства
Чтобы решить квадратные неравенства вспомним, что такое квадратичная функция? Квадратичная функция – это функция записанная формулой : y=ax2+bx+c, где x – независимая переменная, a, b...
Линейные неравенства.
Линейные неравенства называются так, потому что в основе лежит линейная функция или формула прямой (y=ax+b). Линейная функция характерна тем, что переменная x находится в числители...
Нужен репетитор по математике (алгебре) или геометрии?
Всем доброго времени суток!!! Репетитор по математике WhatsApp на номер +79831997608 Вам нужен репетитор по математике (алгебре) и геометрии дистанционно (онлайн)? Вы боитесь, что ваш...
Умножения рациональных чисел, математика, примеры.
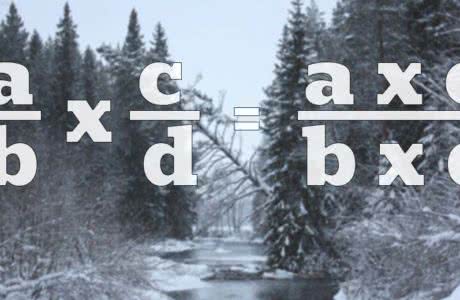
Произведение или умножение рациональных чисел вычисляется так же, как и обыкновенных дробей, разница лишь в знаках. В математике есть понятие умножение рациональных чисел и умножение...